벡터(Vector)
벡터는 사물의 움직임을 프로그래밍하기 위한 가장 기본적인 구성 요소이다.
C++ 프로그래밍에서 벡터(std::vector)는 유동적으로 크기 조절이 가능한 배열 자료 구조를 구현한 것을 말한다.
하지만 이것은 프로그래밍 면에서 바라본 벡터의 정의이고 물리적 관점, 수학적 관점에 따라서 정의가 달라진다.
보통 수학적 관점으로 크기와 방향을 모두 가지는 어떤 양을 벡터라 한다고 정의되어 있다.

위 이미지처럼 점 A에서 점 B로 향하는 벡터가 있다. 여기서 점 A를 시점, 점 B를 종점이라고 부른다.
원래는 벡터 AB의 기호는 밑에처럼 AB 위에 →가 있는 형태이지만, 지금부터 편의상 A→B로 나타내겠다.

벡터의 길이를 벡터의 크기라고 말하며, A→B의 크기를 나타내는 기호는 |A→B|와 같이 나타낼 수 있다.
크기가 0인 벡터를 영벡터 0→로 나타내며, 길이가 1인 벡터를 단위 벡터라고 말한다.
단위 벡터(unit vector)
크기가 1인 벡터를 단위 벡터라고 말하며, 다음과 같이 정의한다고 한다. 여기서 sgn은 부호 함수를 말한다.
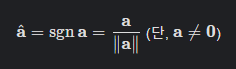
a 위에 있는 꾸밈 기호 ^는 햇(hat), 또는 캐럿(carot)이라고 읽는다.
스칼라(scalar)
스칼라는 크기와 방향을 가지는 벡터에 대비되는 개념으로, 크기만 있고 방향을 가지고 있지 않는 양을 말한다.
일반적으로 크기를 나타내는 수에 단위를 붙여서 그대로 사용이 가능하여, 스칼라의 연산은 일반적인 사칙연산이
모두 적용된다.
여기서 우리가 구하는 벡터의 길이가 스칼라 값을 말하고 있다.
||v|| = √v0² + v1² + v2² + ... + vn²
정규화(normalization)
벡터의 정규화는 어떠한 벡터를 벡터의 길이로 나누어서 그 벡터의 길이를 1로 만드는 것이다.
위에서 봤듯이 길이가 1인 벡터를 우리는 단위 벡터라고 불렀다.
v를 어떤 값을 가진 벡터라고 가정하고, 아래와 같은 공식을 통해서 정규화할 수 있다.
(x / ||v||, y / ||v||, z / ||v||)
쉽게 말해 각 요소들을 벡터의 크기로 다 나누는 것이다.
그런데 이렇게 정규화를 거쳤다고 정규화된 값이 무조건 1이 되는 것이 아니라, 1에 근사한 값을 얻기 위함이다.
보통 우리가 이런 방식을 통해 길이가 1이 된 벡터는 캐릭터의 이동과 방향에 주로 사용한다고 한다.
보통 키보드로 조작하는 방식의 게임은 wsad 또는 방향키를 통해 움직일 것이다.
그런데 여기서 이동키 두 개를 동시에 눌렀을 때 속도가 빨라지는 문제가 발생하는데 이러한 문제를 막기 위해서 정규화를
통하여 이동 벡터의 길이를 1로 맞추어주는 방식이다.
이러한 방식을 자주 사용한다고 하니 기억해두면 좋을 것 같다.
벡터의 합연산
대응되는 스칼라 값끼리 더해서 새로운 벡터를 만들어낼 수 있다.
흔히 두 벡터 중 하나를 평행 이동시켜 평행사변형을 그리는 것이 있는데, 덧셈의 방식에는 크게 삼각형법과 평행사변형법이 있다.
a + b = (a₁ + b₁, a₂ + b₂, a₃ + b₃)
예시로 밑의 이미지의 a→ 종점과 b→ 시점을 일치시켰을 때, a→ 시점을 시점으로, b→ 종점을 종점으로 하는
벡터(A→C)를 a→와 b→의 합이라 하고, (a→) + (b→)으로 나타낸다.

벡터의 곱 연산
벡터의 곱셈에는 내적과 외적이 있다.
내적(inner product)
내적은 벡터의 특정 방향, 성분, 투영(사영)의 크기, 일의 크기 등을 구할 때 사용한다고 한다.
쉽게 말해 두 벡터의 사이각을 알아내는데 유용하다는 것이다.
스칼라곱(scalar product)이라고도 말하며, 두 벡터의 크기와 두 벡터 사이의 각의 cosθ값을 곱한 것으로 정의한다.
A * B = |A| |B| cosθ
그리고 단위 벡터를 사용하면 다른 방법으로도 내적을 구할 수 있다.
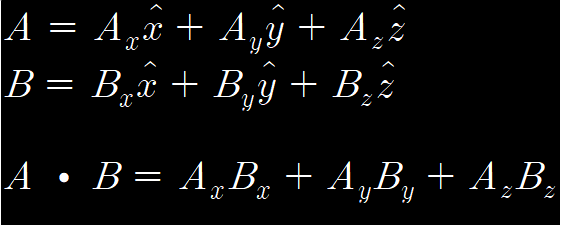
내적은 교환 법칙이 성립해서 A * B = B * A이다.
A * B = (|A| cosθ) |B|
이는 기하학적으로 다음과 같은 의미를 가진다.

따라서 벡터의 내각은 임의의 벡터의 특정 방향을 가진 성분의 크기를 알아내는 데에 유용하다.
외적(outer product)
외적은 면 벡터의 표현, 토크, 각속도 등을 구할 때 필요하다고 한다.
두 벡터에 수직인 벡터를 구하거나, 한 평면의 법 선 벡터(수직인 벡터)를 구할 때 유용하다.
벡터곱(vector product)라고도 하며, 두 벡터의 크기와 두 벡터 사이의 각의 sinθ값, 수직인 벡터의 곱으로 정의한다.
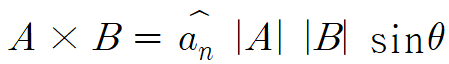
여기서 an은 A와 B에 서로 수직인 벡터를 말하는데, 때문에 외적은 내적과는 다르게 3차원 공간에서 정의가 된다.
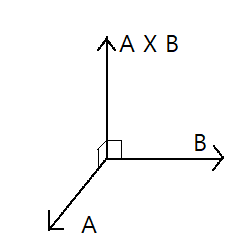
외적은 교환 법칙이 성립하지 않지만, 방향이 반대로 된다.
A × B = -B × A
참고자료
벡터의 곱셈(내적과 외적)
벡터의 곱셈에는 내적과 외적이 있다. 1. 내적(inner product) 내적은 벡터의 특정 방향, 성분, 투영(사영)...
blog.naver.com
벡터 - 나무위키
체(field)[6] F F F에 대해, 집합 V V V가 "체 FFF위의 벡터 공간(vector space)"이라 함은, V V V가 F F F의 F F F-가군(module)인 것이다. 이를 풀어쓰면 다음과 같다. 그리고 이 때, FFF를 VVV의 스칼라라고 한다.(가
namu.wiki
벡터(vector)란?
그래픽스에 선형대수가 많이 사용된다고 하셔서 .. 이미 수강했지만 정말 다까먹었으므로 좋은 유튜브 강의를 보면서 다시 공부하고 기억을 다시 떠올리는 의도로 벡터란 무엇인가? 여기에는
iagreebut.tistory.com
벡터란? (개념 이해하기) | 벡터 | Khan Academy
수학, 예술, 컴퓨터 프로그래밍, 경제, 물리학, 화학, 생물학, 의학, 금융, 역사 등을 무료로 학습해 보세요. 칸아카데미는 어디에서나 누구에게나 세계 최고의 무료 교육을 제공하는 미션을 가진
ko.khanacademy.org
수학 공식 | 고등학교 > 벡터의 뜻과 연산
벡터의 정의 크기와 방향을 가지는 양을 벡터(vector)라 한다. 점 $ {A} $에서 점 $ {B} $로 향하는 벡터가 있다고 할 때, 점 $ {A} $를 시점, 점 $ {B} $를 종점이라 하고, 기호로 $ \overrightarrow{{AB}} $와 같이
www.mathfactory.net
벡터 - 길이와 각도(스칼라 적)
길이, 거리, 각의 벡터적인 의미는 두 벡터의 스칼라적의 표현을 사용하여 나타낼 수 있다. $\overrightarrow u$와 $\overrightarrow v$의 스칼라적 : $\overrightarrow u\cdot\overrightarrow v = u_1v_1 + u_2v_2+\cdots+u_nv_n(\
codingfarm.tistory.com
벡터 크기의 이해와 정규화 과정
오늘부터 게임 개발에 필수적인 벡터에 대해 공부하면서, 배운 내용을 블로그에 정리해보겠다. 첫 포스팅은 벡터의 크기와 정규화 과정에 대해 이해해보겠다. 벡터의 크기 벡터의 크기는 곧 기
ballbot.tistory.com
[Math] 정규화 (1) - 벡터와 좌표의 정규화
안녕하세요! 여러분들과 함께 게임 개발을 공부하는 베르입니다! 이번 영상에서는 개발할 때 활용할 수 있는 정규화라는 개념에 대해서 알아봅시다! 타임라인 0:00 인트로 0:10 정규화란? 0:47 벡터
wergia.tistory.com
'수학' 카테고리의 다른 글
| 행렬의 종류 (0) | 2022.12.15 |
|---|---|
| 삼각비, 삼각함수 (0) | 2022.12.07 |
| 호의 길이(라디안) / 부채꼴 (2) | 2022.10.13 |
| 라디안이란?(radian) (0) | 2022.10.12 |
| 호의 각도 / 호의 길이 (0) | 2022.10.11 |



